一,數學最重要的問題與物理最重要的問題可以結合嗎
[color=inherit !important]数学最重要的问题与物理最重要的问题可以结合吗----中科院科学智慧火花idea.cas.cn/viewdoc.action?docid=55156
(一),千禧年數學問題
對於千禧年7個數學問題,為什麼這七個問題被選中超過其他問題,更具體地,為什麼霍奇猜想(Hodge猜想)被包括。 一些問題是整個研究領域的基礎:
1,P與NP是電腦科學的聖杯,
2,納維葉-斯托克斯存在性與光滑性(Navier-Stokes)是流體力學的基礎,
3,Yang-Mills理論是粒子物理的基礎。
其中三個與數學中的概念有關:
4, 解決黎曼猜想(Riemann假設)為更好地理解素數鋪平了道路,
5,貝赫和斯維訥通-戴爾猜想(Birch和Swinnerton-Dyer猜想)是關於確定是否有一個簡單的方法來區分有限和無限解的多項式方程,這意味著什麼?
6,而龐加萊猜想(Poincaré推測)與3d表面如何工作有關。
(二),霍奇猜想有什麼呢?
人類一直在研究形狀的數學,直到一個三角形在西元前500年前第一次被畢達哥拉斯注意。 經過幾代人,研究越來越複雜的形狀,直到大約兩千年後,各種幾何形狀看起來像蒸汽。 數學家已經做了所有他們可以想到的形狀,並沿途提供了一切從工程到透視繪畫的基礎(特別是天才的達芬奇)。
然後,在1637年,一個聰明的年輕數學家哲學家笛卡爾認識到,如果你抽象一步,幾何實際上是與代數相同。笛卡爾做了很多思考幾何線如何只是一組數字。 方程也可以產生一組數字作為它們的解。 如果這兩組數字完全相同,則在一張紙上繪製的線可以被認為是與等式的解的相同的東西。這是數學中的分水嶺時刻,它允許代數中開發的所有工具應用於幾何。 這就是為什麼你的學校數學老師對將線性圖轉換為方程式感到如此興奮:任何隨機線可以被認為是一個等式的解集,例如y = mx + c。
任何圓是一組解決方案
到現在,如果你想看到某條線與特定圓交叉的位置,你可以幾何地繪製形狀,或者只是用代數方式比較方程。 兩種方法都會給出相同的答案。數學家不滿足於,他們很快發現更複雜的方程,或者甚至方程組都在一起工作,可以在各種維度產生驚人的形狀。
一些仍然可以被形象化的形狀 ,例如方程組的解決方案映射出一個環的表面,被稱為環面 。但其中許多是超出了我們可以畫,只有通過代數和一個非常伸展的想像力。由於數學家現在正在處理超出我們可以想像的對象,這些“形狀”通常被稱為“代數迴圈”。 如果一個代數週期是一個不錯的流暢,一般乖巧的造型,它也獲得稱號“總管” 。
第一:一組數學家知道,拓撲學家開始看看如果你在多面體上繪製形狀會發生什麼。 你可以想像你有一個環形甜甜圈,你在頂部畫一個三角形。 或者五角大樓。其實,你需要兩個? 如果形狀可以滑動和拉伸,則三角形可以扭曲成五邊形。 拓撲學家將所有可能從一個變形到另一個(沒有從歧管表面扯起)的形狀分組成“同源性類” - 一種廣義形狀。 所有通過甜甜圈的“孔”的形狀將形成不同的同源性類別。
第二,一群代數學家開始採用已經產生好的整理流形並添加更多方程的方程組。 這些附加方程在這些歧管內產生新的代數迴圈。不久之前,人們意識到拓撲學家將同源性類繪製到歧管上,代數學家將代數迴圈嵌入到歧管中實際上是同樣的事情。 這是當幾何形狀首先遇到代數方程時的重複。 困難是沒有人知道當歧管上的同源性分類包含至少一個也可以描述為代數迴圈的形狀。
總而言之,歧管是可以通過一組方程描述的奇怪(可能是高維)形狀。 添加額外的方程將給你更小的形狀,稱為代數迴圈,在該流形。
問題是:如果你把任何隨機的可能的討厭的形狀繪製到一個歧管上,你怎麼知道它是否可以被拉伸成一個不同的形狀,可以被描述為一個好的代數迴圈?
(三),霍奇的想法
蘇格蘭數學家威廉·霍奇:怎麼能知道哪些類的同源性在任何給定歧管,相當於一個數學週期?

霍奇
一個偉大的想法。 只是他不能證明。 我們有一個小的平滑的“空間”(在每個鄰域類似於歐幾裏德空間,但在更大的規模上,“空間”是不同的),這是由一群方程描述,使得這個空間具有均勻的維度。 然後我們獲取基本的“拓撲”資訊,並將其分解成更小的幾何部分(由數字對標記)。
幾何部分內的理性東西被稱為“Hodge迴圈”。 每個較小的幾何部分是稱為代數迴圈的幾何部分的組合。 基本上我們有一個“樁”。我們仔細看看它,看看它是由許多“切碎的木材”組成。“切碎的木材”裏面有“twigs”(霍奇迴圈)。
霍奇猜想斷言,對於成堆的切碎的木材,樹枝實際上是被稱為原子(代數迴圈)的幾何部分的組合。
1958年,英國數學家,第13次國際數學大會的主席,W.V.D.Hodge霍奇教授提出:對於射影代數簇空間,在非奇異複射影代數簇上, 任何一個霍奇類都可以表達為代數閉鏈類的有理線性(幾何部件的)組合。
這個叫霍奇猜想的東東,用通俗的話說,就是“再好再複雜的一座宮殿,都可以由一堆積木壘成”。
用文人的話說就是: 任何一個形狀的幾何圖形,不管它有多複雜(只要你能想得出來),它都可以用一堆簡單的幾何圖形拼成。
二十世紀的前半葉,數學家希望得到研究複雜形狀的方法。基本思想是:任何一個複雜形狀都可以由一組簡單的幾何形狀基本模組粘合形成。這是極其傳統的數學方法.也是千年來歐幾理得幾何公理系統的原始思想。
問題是在什麼程度上(過程到底有多複雜),對於給定的複雜形狀,我們可以通過把維數不斷增加,把越來越多的簡單幾何基本模組粘合在一起,來形成該複雜形狀。數學家希望用這種思想,用各種不同類型的方式一步一步地擴展,最終建立一組強有力的代數方程或/和幾何工具,使各種複雜的對象分類成一些具體的簡單的幾何對象及其組合。在這種擴展過程中,幾何出發點變得模糊起來——到底從那些簡單幾何對象組合起;組合的程式/序列又是什麼。因此,必須加上一些沒有任何幾何解釋的"非幾何"基本模組。以期達到:在非奇異複射影代數簇上, 任何一個霍奇類對象都可以表示為代數閉鏈類的有理線性組合,這就是著名的霍奇猜想。
(四),我們構造的例子
構造一個有無窮多個兩兩相連區域的空間結構,也是霍奇猜想的一個標準例子
圖A
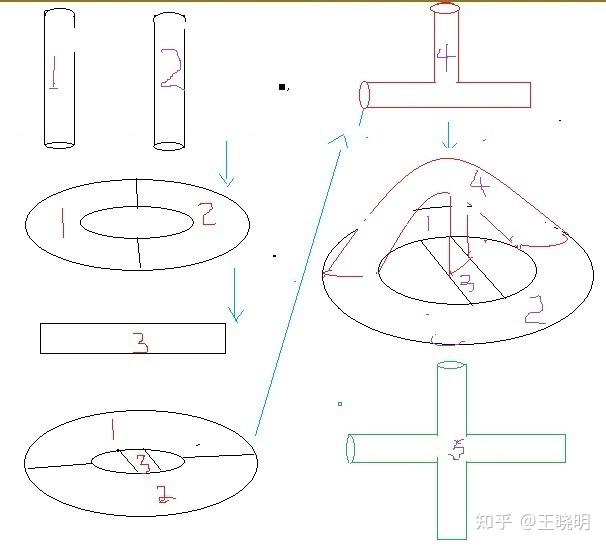
圖A-1,兩根管子,一個記為1,一個記為2。
圖A-2,兩根管子端端相連形成一個象汽車輪胎一樣的環,有2個區域兩兩相連。
圖A-3,再把一根管子記為3,一頭安插在區域1,一頭安插在區域2.於是有3個區域兩兩相連,圖A-4。
如法炮製,圖A-5,用三叉管子記為4,一頭安插在區域1,一頭安插在區域2,,一頭安插在區域3.於是有4個區域兩兩相連。
圖6,用四叉管子記為區域5,按照以上步驟,分別安插在1,2,3,4,區域。它有5個區域兩兩相連。
我們可以無限制進行下去,5叉,6叉......構造無窮多個兩兩相連區域。
這是霍奇猜想提出80年以來第一個構造的例子。
(五),這個例子有什麼用?
我們的世界
如果您關心我們的宇宙,關心物理學就會清楚,我們的宇宙被兩種理論主宰:
一個是行星繞著太陽轉時,就像籃球放在床單上,當球移動時,床單就會變形,這個就是大品質物體如何扭曲時空的理論。
另外一個是量子理論,它解釋了微觀世界不可思議的事情,為什麼光既是粒子也是波。
量子糾纏是兩個粒子之間的鏈接,一個粒子的狀態影響另外一個粒子的狀態。
如果按照第一種理論,引力支配一切,這些粒子應該表現不同,就不會有量子糾纏。
上面這個問題困擾著物理學家。
(六),Mark Van Raamsdonk理論
加拿大英屬哥倫比亞大學一位叫做Raamsdnk的物理學家,
图B

·
在多次投稿失敗以後,最終在【廣義相對論和引力學】2010年10月,發表了自己的論文【用量子糾纏建立時空】
图c

,
Raamsdnk整合了兩大理論,認為時空不過是量子系統中物質糾纏狀態的幾何,叫做張量網路,宇宙建立的網路就像樹枝朝不同方向生長一樣,宇宙不會膨脹也不會收縮,兩個粒子的鏈接並不存在引力,而是像蟲洞一樣。幾何引力的空間模型就能解釋量子糾纏。(不熟悉這個問題的人可以在科學網輸入“MARK van Raamsdnk”就可以瞭解)時空就是量子系統物質糾纏狀態的幾何圖像,稱為反德西特空間。
問題是:如果宇宙象樹枝一樣,這棵樹的任意兩個區域或者兩個點,如果不是兩兩相連,兩個粒子的聯繫就會被堵住,也容易被阻斷,可以通過試驗來證實一下。
(七),霍奇猜想與廣義相對論量子糾纏龐加萊猜想融為一體
如果是兩兩相連的管道,當然無法阻斷,Maldacena和Susskind的猜想是,如果任何兩種粒子存在糾纏現象,那麼它們則會有效地存在於一個蟲洞
為什麼兩兩相連的幾何網路下量子糾纏可以存在?因為任何兩個區域都是相連的,在任意兩個區域的一個粒子和另外一個區域的粒子當然也是區域兩兩相連,只不過一個粒子是另外一個粒子的鏡像而已,在A區域的粒子如果是左旋,例如左手套,右旋右手套在B區域。兩個區域的兩個粒子就是互為鏡像,絕對不會是一樣的。一個人在鏡子面前就是這樣的理解。多個量子糾纏就是多個區域的兩兩相連,例如一個人四面六方都安裝了鏡子,就會有六種不同的鏡像。對於兩兩相連區域,量子糾纏就是理所當然的了,根本無需驚奇。
Maldacena和Susskind的猜想是,如果任何兩種粒子存在糾纏現象,那麼它們則會有效地存在於一個蟲洞內。黎曼幾何為愛因斯坦相對論提供了幾何模型,兩兩相連區域理論將完善van Raamsdnk理論。
物理學家是否接受?還要看是否與實際符合。
但是,現在看來,這個模型比卡拉比丘成桐模型更加接近,因為,卡拉比丘成桐模型沒有解釋量子糾纏。